来自本学期的《工业机器人系统》课程实验,使用工业机器人实现五子棋人机对弈,同时收录为人类早期战胜 AI 珍贵影像👍
硬件
- 埃夫特 ER3A-C60
- 埃夫特紧凑型控制柜
- 固高示教器
- Basler acA1300-30gm 相机
方案
使用吸盘作为工业机器人末端执行器,完成棋子取放工作;使用标定后的工业相机实现定位;使用 OpenCV 的模板匹配实现棋子识别;使用 AlphaZero_Gomoku 方案实现决策系统;使用 3D 打印实现棋子供料(未完成)。
本人在实验中主要负责了相机标定、手眼标定等相关模块,下文针对性地整理记录一些经验,不过多涉及其他部分。
前序知识
(1)世界坐标系(Xw,Yw,Zw):在环境中由用户任意选择一个基准坐标系作为参考来描述摄像机位置,在相机标定中一般选择标定板坐标系作为世界坐标系。 (2)摄像机坐标系(Xc,Yc,Zc):以针孔模型的聚焦中心 O_c(光心)为原点,摄像机光轴为 Z 轴建立三维坐标系,其中 Xc轴、Yc轴与成像平面 x、y 轴平行。光心到图像平面的距离为有效焦距 f。 (3)成像平面坐标系(x,y):光轴与成像平面交点,称为主点。成像平面坐标系以主点为原点,是以物理单位表示的平面直角坐标系。 (4)图像坐标系(u,v):固定在图像上以像素为单位的平面直角坐标系,通常以图像左上角为像素原点,每一像素的(u,v)分别表示该像素在图像数组中的行数和列数。u、v 轴分别与 x、y 轴平行,该坐标系的单位为像素。
相机标定
摄像机采集的是二维图像,需要通过摄像机成像几何模型建立目标物体的 3D 坐标和 2D 图像坐标之间的关系,该模型参数就是摄像机标定所确定的内外参数。
图像坐标系到相机坐标系的转换关系为: $$ Z_{c}\left[\begin{array}{l}u \v \1\end{array}\right]=\left[\begin{array}{ccc}f_{x} & 0 & u_{0} \0 & f_{y} & v_{0} \0 & 0 & 1\end{array}\right]\left[\begin{array}{l}X_{c} \Y_{c} \Z_{c}\end{array}\right] $$
保持机器人末端位姿不变,手持并改变标定板的位姿,连续拍摄多张照片,导入到 MATLAB 的 Camera Calibrator 工具箱,使用张正友平面法即可标定。
 改变标定板位姿
改变标定板位姿工具箱同时还提供了标定结果的可视化界面,可以非常直观地看到标定效果,同时也可以与 RotationMatrices 和 TranslationVectors 矩阵对比,进一步理解平移矩阵和旋转矩阵。
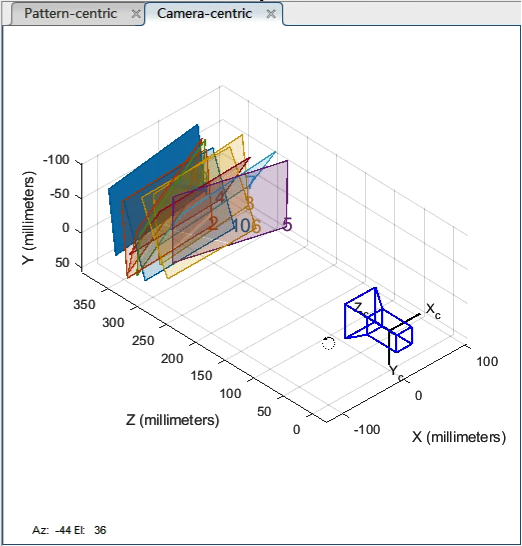 可视化结果
可视化结果导出相机内参矩阵: $$ \mathrm{IM}=\left[\begin{array}{ccc}2884.23675583725 & 0 & 1286.85887766546 \0 & 2883.28824430723 & 977.912424612791 \0 & 0 & 1\end{array}\right] $$
手眼标定
摄像机标定所得的是目标在摄像机坐标系下的坐标,而控制机械臂运动往往需要的是目标物体在机器人坐标系下的坐标,因此我们还需要进行手眼标定,得到摄像机与工具手之间的空间关系,实现工件抓取。
首先建立整个系统坐标系模型:G 为末端执行器(工具手)坐标系,B 为标定板坐标系,C 为摄像机坐标系,W 为机器人坐标系。易得:
$$ _b^wT=_g^wT _c^gT _b^cT $$
$_b^wT$为标定板相对于机器人的位姿关系,当标定板不动时,$_b^wT$为定量保持不变;$_g^wT$是执行器相对于机器人的位姿关系,由机器人控制器给出;$_c^gT$是摄像机相对于末端执行器的位姿关系,即为手眼标定所求量;$_b^cT$是标定板相对于摄像机的位姿关系,即摄像机标定所得的外参。
保持标定板不动,机器人运动到两个不同的位置下,由$_b^wT_1$和$_b^wT_2$相等可得等式:
$$ {_g^wT_1} {_c^gT} {_b^cT_1}={_g^wT_2} {_c^gT} {_b^cT_2} $$
可以写成以下形式: $$ AX=XB $$
其中: $$ A=(_g^wT_2)^{-1} {_g^wT_1}, B={_b^cT_2} (_b^cT_1)^{-1}, X=_c^gT $$
易知,A 为工具手两次运动对应变换矩阵,B 为摄像机两次运动对应的变换矩阵。标定问题转化为解该矩阵方程的问题。为了实现唯一解,需要知道两组 A 和 B,需要 3 个位置的摄像机标定结果。
此时保持标定板不动,改变机器人末端位姿,拍摄三张照片并分别记录下末端在机器人坐标系下的坐标。
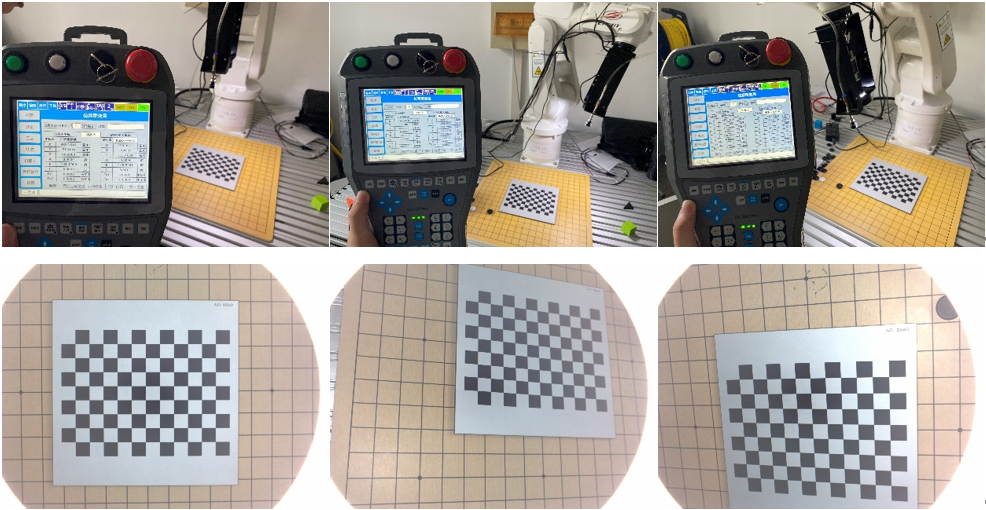 手眼标定
手眼标定然后将三张图片导入 Camera Calibrator 工具箱,计算外参。编写程序计算 Tch 矩阵,主要参考的教程来自 基于视觉伺服的工业机器人系统研究(摄像机标定、手眼标定、目标单目定位),需要自己补充欧拉角到旋转矩阵的转换以及数据初始化相关的代码。
由于一开始数据记录混乱,实验时对原理的掌握也不深刻,自己在这部分程序调试上花费了不少时间。主要踩过的坑有:示教器中世界坐标系的原点是可以人为设定的,因此会与机器人坐标系存在一定的差距,所以这里用到的坐标与欧拉角一定要在示教器的机器人坐标系下;欧拉角转换成旋转矩阵的时候注意角度与弧度的变换、XYZ 乘法顺序;MATLAB 求解出的内参矩阵、外参旋转矩阵矩阵需要转置,而示教器中的欧拉角 ABC 是直接对应 XYZ 的。
最后计算出的结果为:
$$ \operatorname{Tch}=\left[\begin{array}{cccc}-0.0060 & -1.0427 & -0.0237 & 16.1604 \1.0158 & 0.0121 & 0.0144 & -44.7796 \0.0010 & -0.0240 & 1.0558 & 68.6513 \0 & 0 & 0 & 1.0000\end{array}\right] $$
观察可以发现,相机与末端的 z 轴近似重合,符合两者都竖直向下的事实;而在 xyz 轴上的偏移量约为 1.6cm、-4.5cm、6.9cm,使用尺子测量核对,发现存在一定的误差。推测是由于图像样本数量太少,导致标定误差较大,后期或许可以增加样本数量,使用最小二乘来求矩阵最优解。
观察公式$_b^wT=_g^wT _c^gT _b^cT$,由于三组样本没有改变标定板在机器人坐标系下的位置,所以理想情况下的 Tch 应该能保证对任意一组样本,等式右侧都相等。但实际代入后,发现误差非常大:
$$ H_1\cdot Tch\cdot C_1=\left[\begin{matrix}-0.0029&-1.0375&0.0124&455.0323\-1.0156&-0.0123&-0.0094&10.1779\0.0237&-0.0120&-1.0505&-31.8727\0&0&0&1.0000\end{matrix}\right] $$
$$ H_2\cdot Tch\cdot C_2=\left[\begin{matrix}-0.1560&-0.9143&0.4673&373.8901\-0.8401&-0.1548&-0.5499&141.1848\0.5644&-0.4673&-0.7517&-82.9623\0&0&0&1.0000\end{matrix}\right] $$
这种验证方法本身没有问题,与其他组别的同学讨论后发现这样的结果并非偶然。
定位
根据目标在图像像素坐标系中的坐标$\left[\begin{array}{l}u \v \end{array}\right]$, 将 u,v,Zc(测量所得)以及内参矩阵代入,可得目标在相机坐标系中的坐标:
$$ \left[\begin{array}{l}X_{c} \Y_{c} \Z_{c}\end{array}\right]=\left[\begin{array}{ccc}f_{x} & 0 & u_{0} \0 & f_{y} & v_{0} \0 & 0 & 1\end{array}\right]^{-1} Z_{c}\left[\begin{array}{c}u \v \1\end{array}\right] $$
而目标在世界坐标系下的坐标就是:
$$ \begin{bmatrix}X_w \Y_w \Z_w \1\end{bmatrix}={_g^w}T\cdot {_c^g}T\cdot \begin{bmatrix}X_c \Y_c \Z_c \1\end{bmatrix} $$
接着对于实际场景进行验证。参考“定位”相关的理论知识,手工测量 Zc,注意其符号需要和手眼标定得到的 Tz 相符;获取到图片后可以使用图像处理软件获取目标棋子的像素坐标,此时要注意图片的原点位置以及正方向,如果不清楚可以选择一个特殊位置点进行测试;然后代入公式一步步进行验算,必要的时候可以代入理想情况下的解(例如旋转矩阵换成单位阵)进行理解、比较。
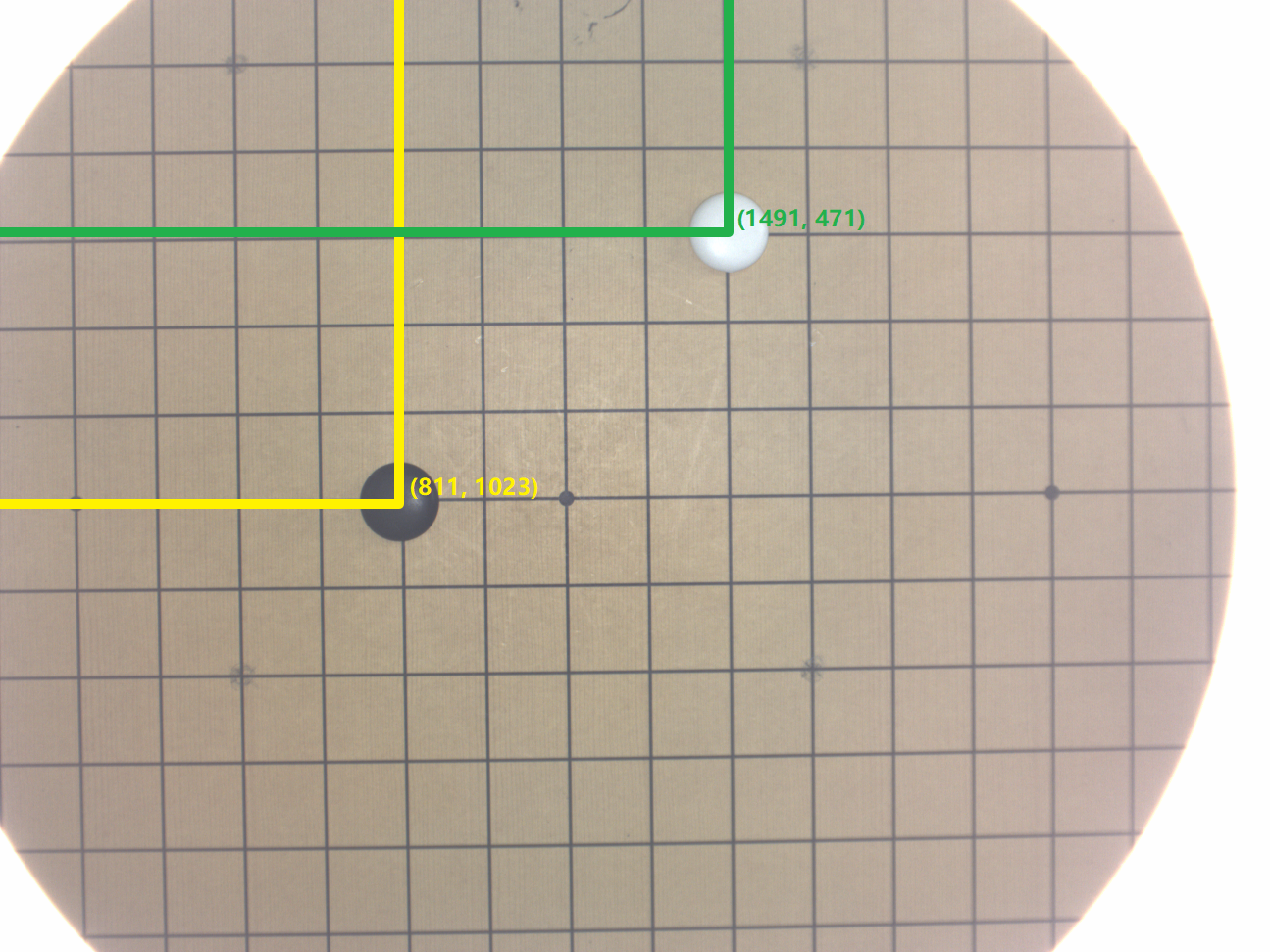 像素坐标系
像素坐标系以黑棋为例,像素坐标为 (811, 1023),代入上文的内参、Tch,将图像坐标系中的黑棋依次转换到相机坐标系、末端执行器坐标系、机器人坐标系下,最后可以得到棋子在机器人坐标系下的位置为
$$ \left[\begin{array}{c}398.2564 \-111.6166 \-9.9233\end{array}\right] $$
标定结果存在有较大的偏差,且远远超出了一个棋盘格的量级,因此这样的标定结果不能用于后续操作。猜测问题可能还是出在手眼标定的精度上,相机的轻微旋转都会对像素坐标造成很大的影响。查阅资料后了解到,除了张正友标定法,还有九点标定法,其对误差修正的效果更好。但由于本次实验时间有限,为了尽快与小组内其他模块对接,我们决定使用人工标定的方法。
由于棋盘位置固定不变,我们手动记录下吸盘末端运行到 (0,0)、(7,7) 等四个角落时的机器人坐标,利用线性插值拟合出棋盘上 64 个点位。这样得到的结果精度尚可,但也只能算一个勉强合格的替代方案。(后续查阅资料时发现这其实就是九点法标定的思想)
总结
本次实验时间非常紧张,但队友们个个身怀绝技,互相帮助,攻坚克难,基本完成了自己一开始设定的提高要求。
应用于棋类游戏的强化学习算法已经有所接触,但是区别于命令行下棋,面对一台高自己一头的机器人时,还是有不少敬畏之心的,毕竟万一机器人生气掀桌就惨了。
验收当天下午机器人和人类进行了数盘激烈对局,最终以 1:2 告负,失败原因还是要归结于不够健壮的识别算法和不够精准的标定系统。