D-H 变换
机器人运动学,主要关心的是机械臂中各个关节变量(转动副中的转动角度或移动副中的移动距离)与机械臂末端位姿的关系。具体来说,正运动学就是已知关节变量,求末端位姿;逆运动学是已知末端位姿,求关节变量。为了用数学的方法描述机械臂,通常使用的一种坐标表示方法为 D-H(Denavit-Hartenberg) 变换,也是本文的一个重要前序知识,详细的定义和公式可以参考教材 1 或其他博客资料,这里不再赘述。
关于 D-H 参数(标准型),分享一段复习时总结的理解:**D-H 参数的目的是把自由度所在的 Z 轴串起来,主要的方法是定义一个 X 轴,从而在 Z 轴之间建立合适的变换关系。**相应的,设置四个参数来组成一套变换:θ表示 X 绕上一个 Z 轴的旋转,d 表示上一个 Z 轴上的偏移量,a 表示 X 轴上的偏移量,α表示 Z 绕 X 轴的旋转。
Robotics Toolbox
本次仿真主要基于 MATLAB 的 Robotics Toolbox 工具箱 2,其在机器人建模、轨迹规划、控制、可视化方面使用非常方便。这里分享一个最近在 Bilibili 大学上看到的比较优秀的教程:手把手教你 MATLAB 机器人工具箱。
下面简单介绍一下一些常用的命令。
机器人模型建立
机器人模型的构建,主要是通过上文提到的 D-H 表示法创建单个杆件,并将杆件进行连接得到机器人对象。默认采用的是‘standard’标准型 D-H 参数,如果选择改进型需要在后面加上‘modified’。
L1 = Link('d', 0, 'a', 0, 'alpha', pi/2);
L2 = Link('d', 0, 'a', 0.5, 'alpha', 0,'offset',pi/2);
L3 = Link('d', 0, 'a', 0, 'alpha', pi/2,'offset',pi/4);
L4 = Link('d', 1, 'a', 0, 'alpha', -pi/2);
robot=SerialLink([L1,L2,L3,L4]);
robot.name='testRobot';
robot.display();
theta=[0 0 0 0];
robot.plot(theta); %显示机器人的图像
其中,Link 命令的参数除了四个基本的 D-H 参数,还可以包含 offset 关节变量偏移量、qlim 关节变量范围、m 质量、r 质心、I 惯性张量、B 粘性摩擦、Tc 静摩擦、G 减速比、Jm 转子惯量等参数,为更精细的设计仿真提供了很大的方便。
 机器人模型建立
机器人模型建立相应地也可以建立一个球坐标机器人,使用teach命令进行示教,拖动左侧的滑块可以实时看到机械臂的运动情况。
L1 = Link('d', 0, 'a', 0, 'alpha', pi/2);
L2 = Link('d', 0, 'a', 0, 'alpha', pi/2);
L3 = Link('d', 0, 'a', 0, 'alpha', pi/2);
L4 = Link('d', 0.5, 'a', 0, 'alpha', 0);
robot=SerialLink([L1,L2,L3,L4]);
robot.name='testRobot';
robot.display();
theta=[0 0 0 0];
robot.teach(theta); %显示机器人的图像
 球坐标机器人示教
球坐标机器人示教PUMA560 作为一个经典的模型,已经被工具箱作为标准机器人收录,可以使用如下命令直接调出:mdl_puma560,同样使用teach进行示教效果如下。
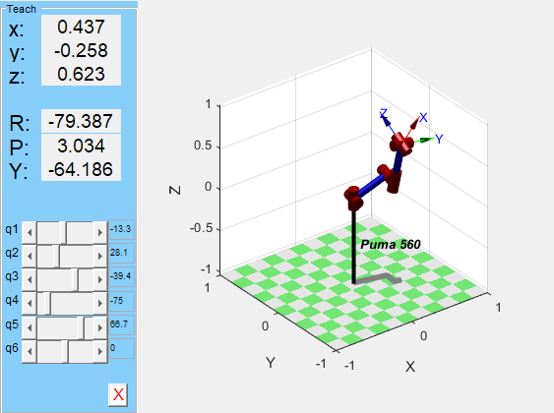 PUMA560 示教
PUMA560 示教正逆运动学求解
工具箱提供了正逆运动学求解的函数:正解fkine,逆解ikine。 以 PUMA560 为例,可以用以下代码进行正运动学求解。
target=[1,1,1,1,1,1];
%target=[0,pi/3,-pi/3,0,pi/4,0];
fkine(p560,target);
p560.plot(target);
为方便验算,选择正运动学求解得到的末端位姿作为目标,使用 fkine 命令进行逆运动学求解,代码如下。
target=[pi/4,-pi/3,0,0,0,pi/6];
p1=p560.fkine(target);
q1=p560.ikine(p1);
不出意外,逆解结果应该和输入的关节变量相等。当出现多解时,意味着机器人可以以多种方式实现这一动作。特别的,当机械臂关节数为 6,腕部三个旋转关节的轴相交于一点,或者满足其他一些特殊构型时 3,可以使用ikine6s函数求封闭解,此时可以由一个或者多个字符来控制运动学位型:左手或者右手 ‘l’,‘r’ ,肘部在上或者肘部在下 ‘u’,‘d’ ,手腕翻转或不翻转 ‘f’,‘n’。
基本轨迹规划
有了正逆运动学,我们就可以指定任意点,让机器人对进行运动学逆解运算,再将分量分解到各关节,驱动末端达到指定位置。这是一种简单的点位运动(PTP),在此基础上我们更希望其实现指定轨迹的运动,即连续运动(CP)。由于在逆解的计算中解析解一般较为困难,一般都是以数值解近似,所以 CP 运动一般是以 PTP 运动为基础,通过在相邻两点之间采用满足精度要求的直线或圆弧轨迹进行插补,来实现轨迹的连续化。
这里展示一个“5-3-5”次多项式插补得到的轨迹规划,分别展示了 PUMA560 的三个关节的位置、速度、加速度,可以看到多项式插补的情况下加速度连续,也就意味着不会造成力的突变。
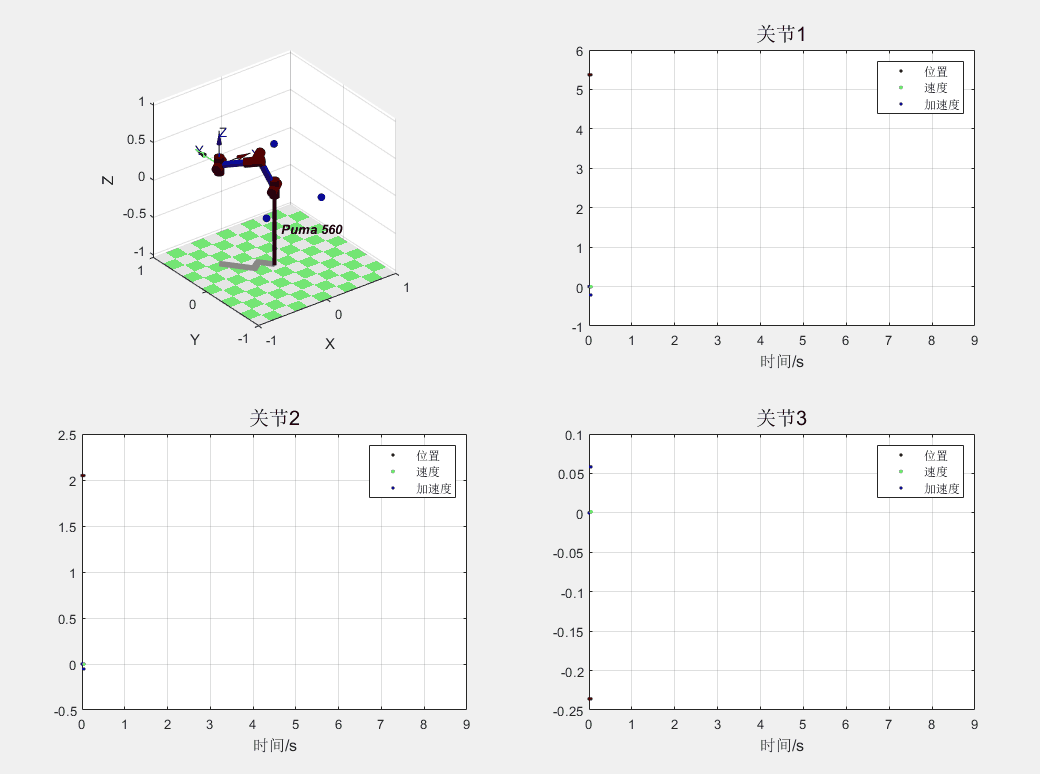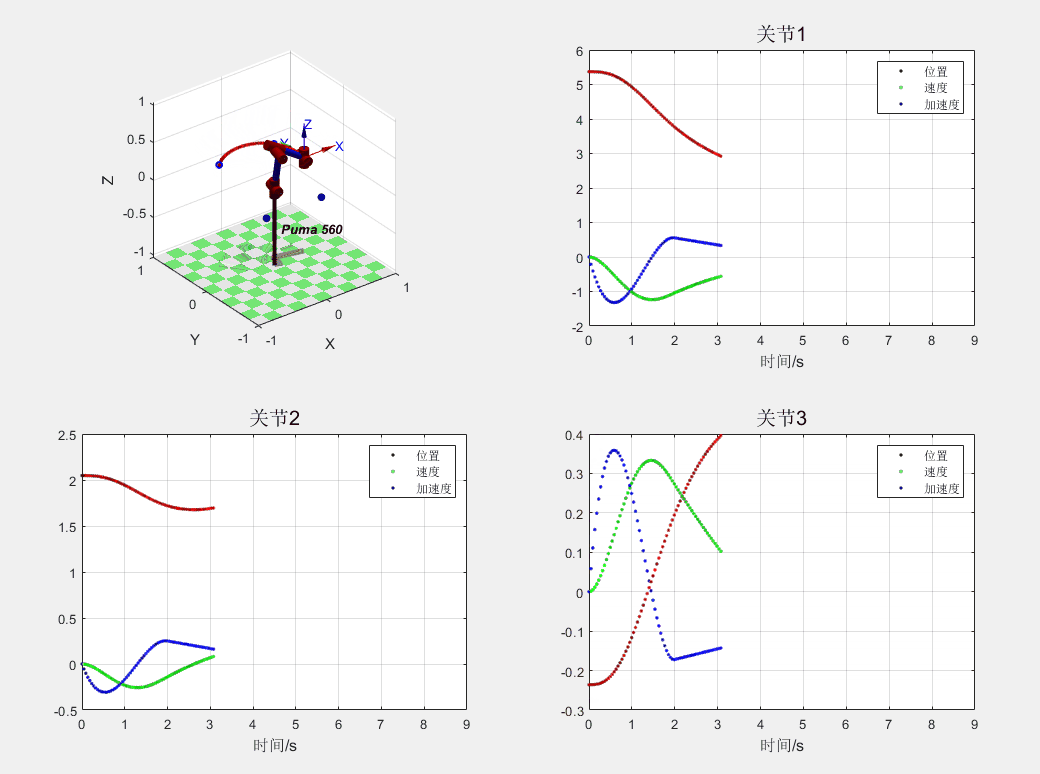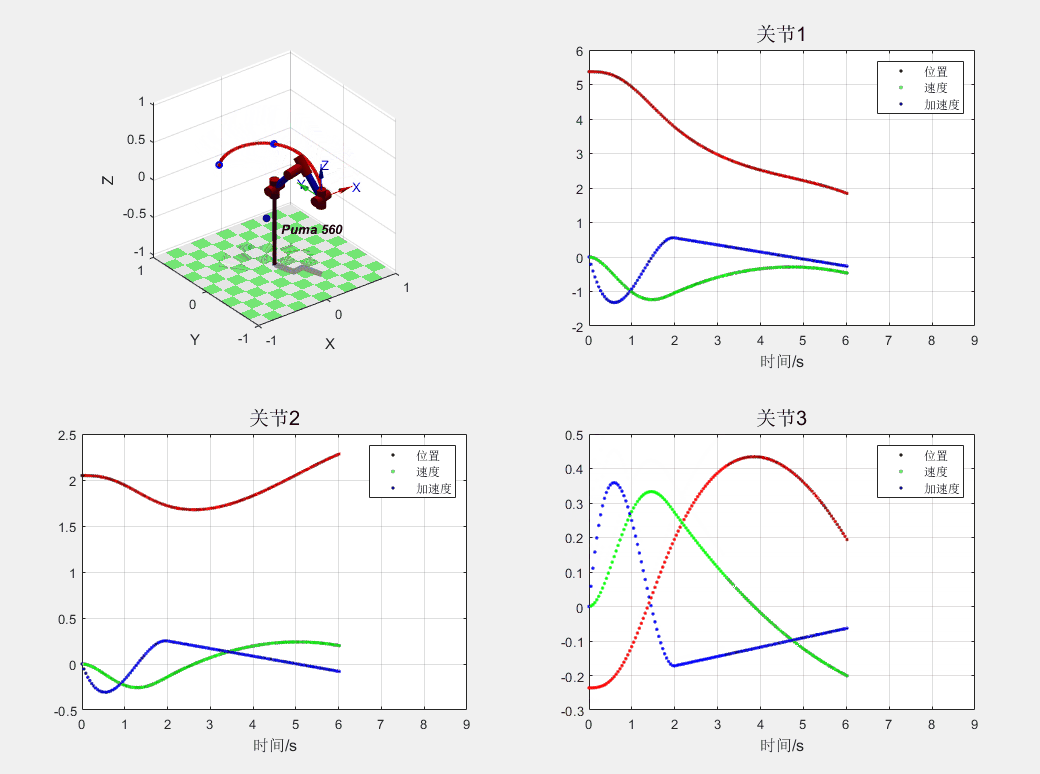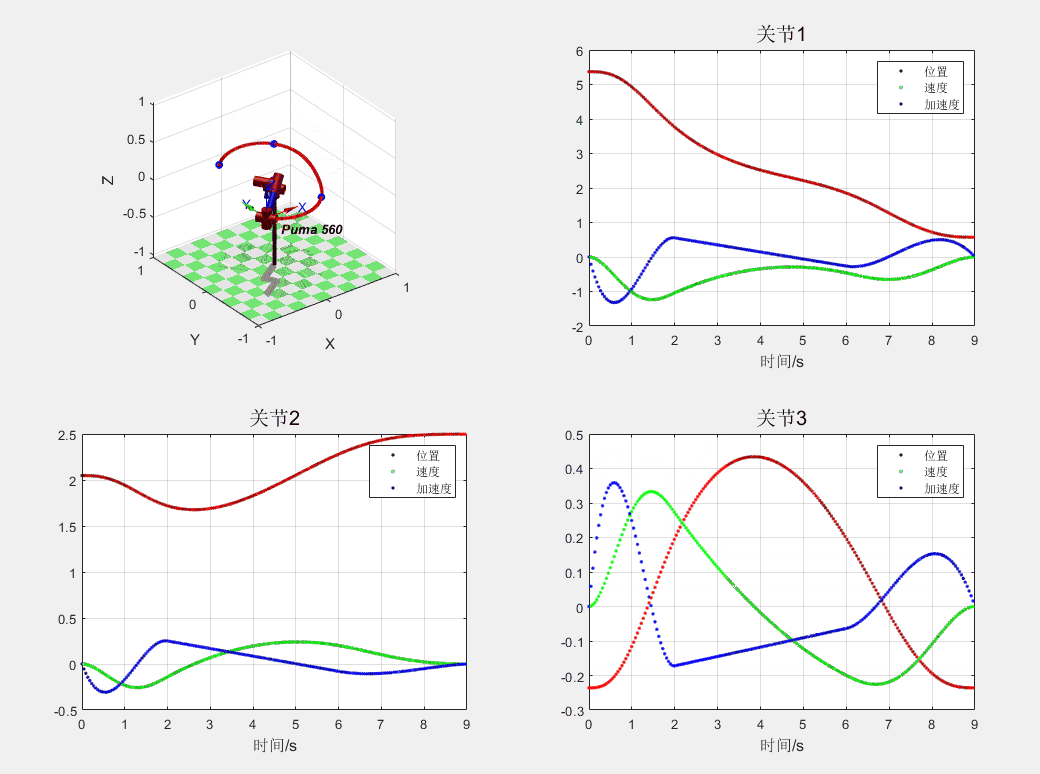 535 多项式轨迹规划
535 多项式轨迹规划水刀运动学模型
接下来将以水刀为例,综合展示一下 MATLAB 机器人工具箱的功能。
水射流切割技术作为一种高新技术,是切割领域的一次革命。水射流切割有着其他切割技术无法比拟的优势:加工能力强,无需打孔,可以在任意点切割,进行任意复杂形状的加工,机构简单,应用灵活;属于冷加工,不产生热形变和金相组织变化,也不产生粉尘,环保无污染,无火灾危害;不产生附加应力变形,尤其是沿切割进给方向和法相方向,切割反作用很小,从而避免了零件由于附加应力而产生的变形。
但同时,水射流切割也有难克服的缺点,主要有切口粗糙、切口纹理弯曲、切口斜面三方面问题,实际生产中可以通过使水刀前倾、偏摆的方法来补偿水射流的切割质量偏差。本次仿真即根据水刀头的模型进行前倾角和偏摆角的计算,模拟其切割过程。
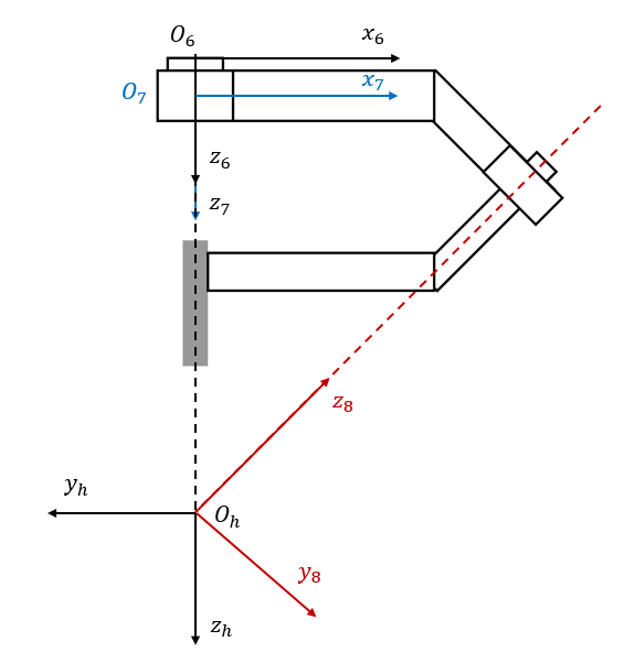 水刀建模
水刀建模首先按照之前的方法建立水刀头的 D-H 模型,对应的参数如下:
| Joint num | ai | di | αi | θi |
|---|---|---|---|---|
| 6-7 | 0 | 0.01 | 0 | 0 |
| 7-8 | 0 | 0.13 | 3/4π | π/2+β |
| 8-h | 0 | 0 | -3/4π | θ |
水刀切割的路径是从输入图片中获取的,经过二值化、边缘检测等操作得到一组离散点列,根据上述 PUMA560 关节末端的活动范围将其缩放到合适比例,得到一个目标路径。接着我们通过这些离散点的前序点计算其所在位置的切线,作为机器人末端坐标系的 x 轴,由此实现末端 z 轴始终保持与切割平面垂直,x 轴始终与切割曲线相切。
这样做可以使得在切割的全程中,水刀只要一开始调整好前倾角δ和偏摆角γ之后便再也不需要驱动水刀的电机,机架末端机构的旋转带动水刀旋转,时时刻刻都保证切割时前倾角δ和偏摆角γ相同,因此水刀的运动与切割图形无关。当切割材料发生改变或者需要切割一个具有固定内切角的材料,需要调整前倾角δ和偏摆角γ时,仅仅需要转动水刀上的电机,而机架末端的位姿和其逆运动学解完全不需要改变。这样的设计真正做到了切割图案和切割方法的完全解耦,机架负责切割图案,水刀负责切割方法和质量。
下图是不带刀头的机架轨迹动画,观察机架末端机构 x 轴,可见其始终与图案曲线相切,z 轴始终保持铅锤。
 水刀机架轨迹规划
水刀机架轨迹规划携带刀头后完整的水刀切割的仿真动画如下,分别展示了三种图案的不同视角。末端执行机构上与 z 轴重合的蓝色长直线代表水射流的方向,在切割过程中水射流方向与设定的前倾角δ和偏摆角γ吻合。
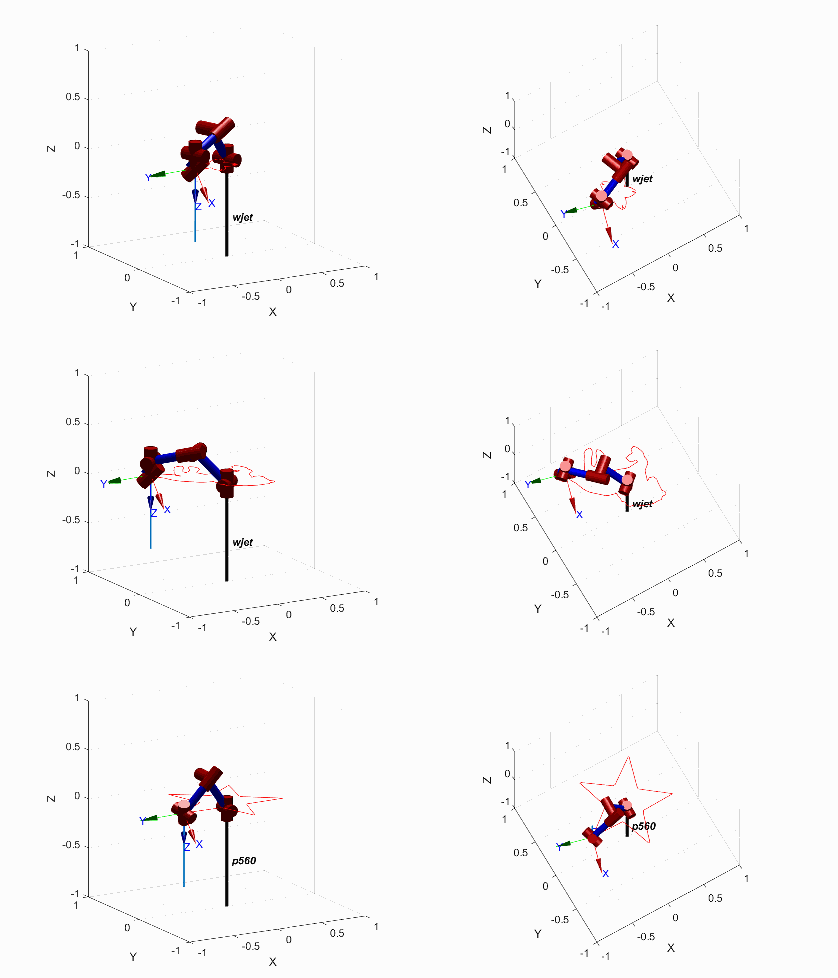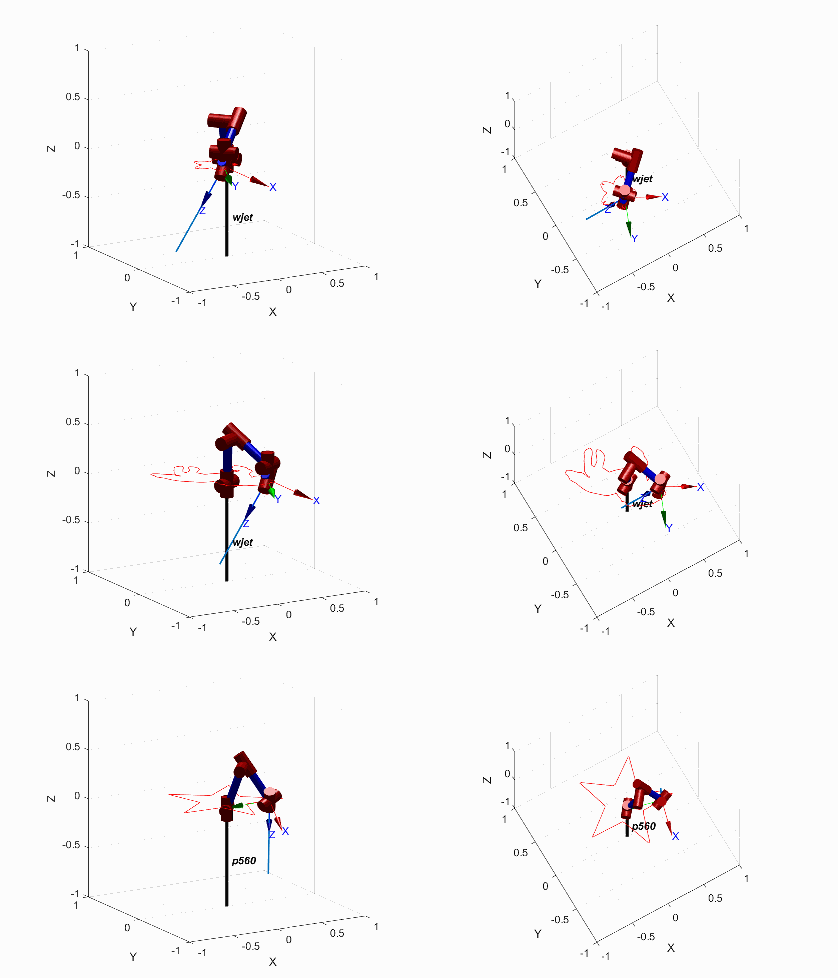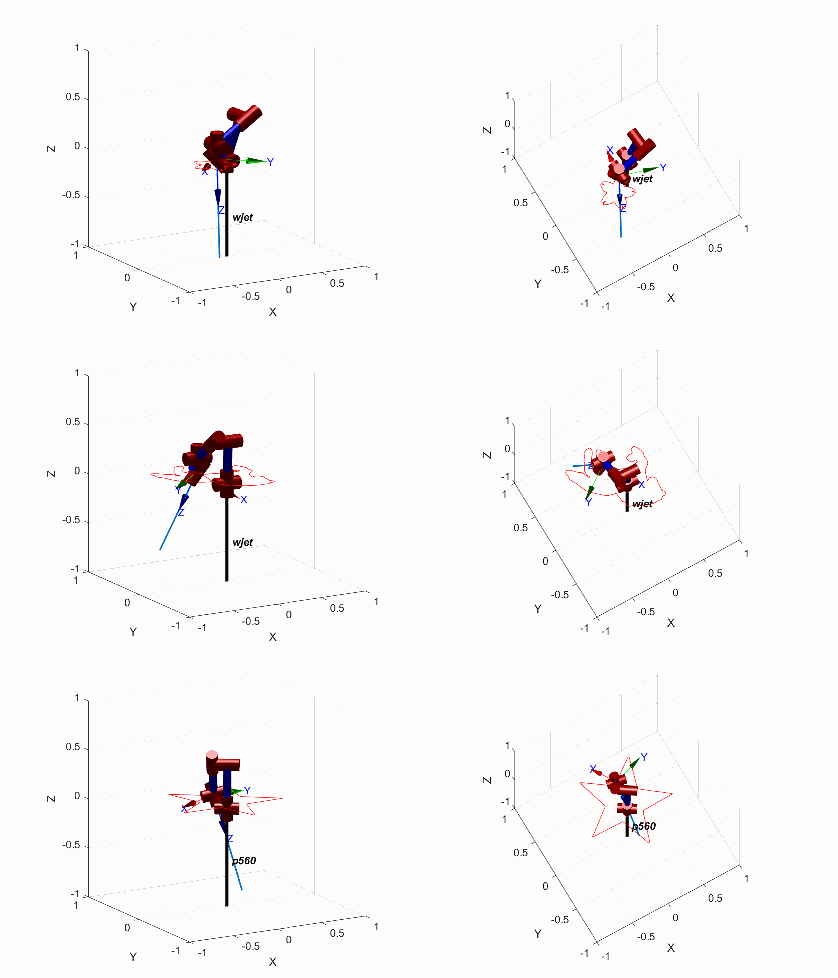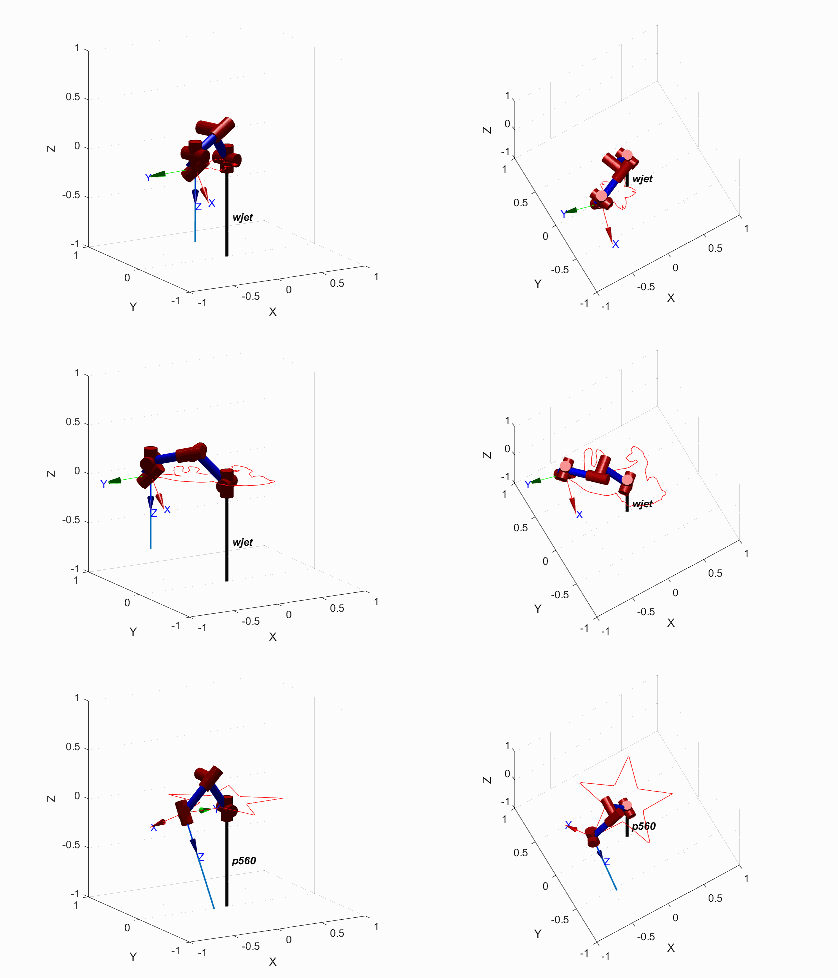 水刀切割动画
水刀切割动画参考资料
- 《机器人学导论:分析、控制及应用》Saeed B.Niku
- Matlab 中 Robotics toolbox 的安装及使用
- ikine6s.m robotics-toolbox-matlab GitHub