比较如下几个问题,求出结果,并谈谈你的见解。 a) 问题 1:李叔叔有两个孩子,两个孩子都是女孩的概率是多少? b) 问题 2:李叔叔有两个孩子,其中一个是女孩,两个孩子都是女孩的概率是多少? c) 问题 3:李叔叔有两个孩子,至少有一个孩子是在星期日出生的女孩,两个孩子都是女孩的概率是多少?
摸鱼的时候看到一个经典概率论题目的变形,标准答案分别为$\frac{1}{4}、 \frac{1}{3}、 \frac{13}{27}$,标准解法不多说了。
很明显,同样一个问题,给出的题干信息不同,求得的概率值不相同。但是仔细观察答案可以发现,限定条件越多,最后的概率越接近$\frac{1}{2}$。想了一会儿,发现可以用图解的办法来解释,很妙。
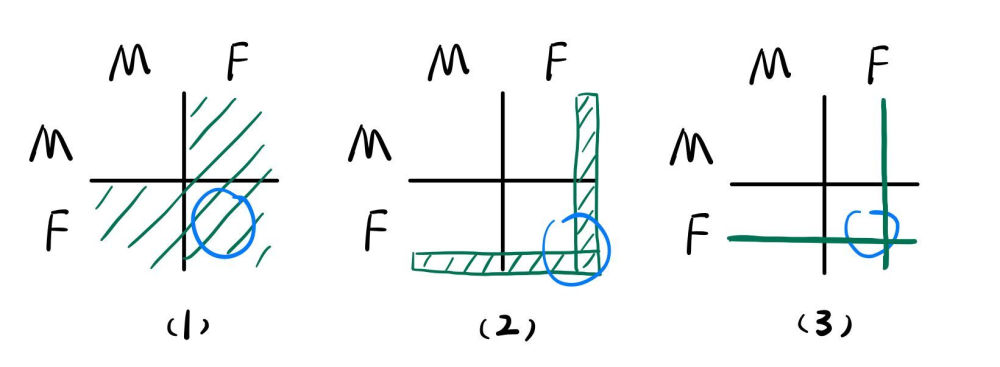
如上图所示:M 表示男孩,F 表示女孩;绿色部分为符合条件的样本空间,作为分母,而蓝色圈出的 (F,F) 象限表示满足“两个都是女孩”条件,两者交集作为分子。
图(1)描述的是“问题 2”给出的情况,因为男孩女孩出生概率均为$\frac{1}{2}$,很明显最后的概率为$\frac{1}{3}$。
图(2)描述的是“问题 3”给出的情况,限定条件“在星期日出生”在 F 区域分别画出了$\frac{1}{7}$区域,最后的概率可以用小学数学$\frac{7+7-1}{14+14-1} = \frac{13}{27}$。
图(3)则试图表示了“限定条件无限多”的情况(此时的题干可以是“其中一位就是三年二班的小红”),两个绿色区域的宽度无限小,所以“两个都是女孩”的概率就可以用线段长度来表示了——$\frac{1}{2}$。
再多想一点,为什么这道题能用图解?其实是因为这题中刚好两个随机变量,可以分别作为 X/Y 轴;如果是三个小孩,那就需要在三维坐标中求体积了。🐵